Thinking about math from someone else’s perspective
"What you do when you’re teaching is you think about other people’s thinking. You don’t think about your own thinking; you think what other people think. That’s really hard." -Deborah Ball
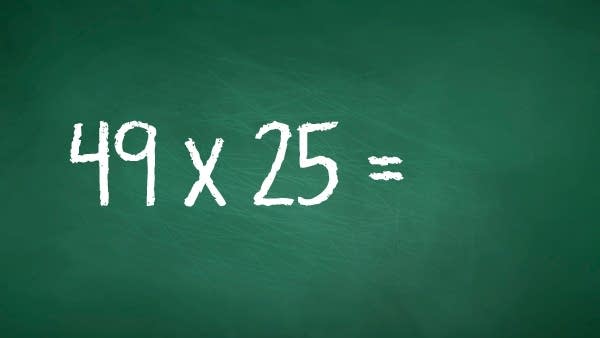
Deborah Ball used to teach elementary school. Now she’s dean of the School of Education at the University of Michigan. She’s on a mission to help the public and policymakers understand what it takes to be a good teacher.
“What you do when you’re teaching is you think about other people’s thinking,” she says. “You don’t think about your own thinking; you think what other people think. That’s really hard.”
Ball has a talk she gives at policy conferences and education events where she illustrates this point by asking her audience to do a math problem.
49 x 25
It’s not hard for a room of adults to figure out the answer.
1225
But then Ball puts up three other answers on a screen.
1485 325 1275
These are answers a teacher might get from fourth-graders who are learning two-digit multiplication. The teacher needs to figure out, on the spot, how did kids come up with those answers? What went wrong? Because to be a good teacher, says Ball, it’s not enough to just tell a kid, ‘that’s the wrong answer.’ And it’s not enough to just show them the right way to do it. There is something the kids don’t understand, and the teacher needs to correct the misunderstanding so it doesn’t happen again.
So, can you figure out what students might have done wrong? What flaws in mathematical thinking could produce these wrong answers?
49 x 25 = 1485?
49 x 25 = 325?
49 x 25 = 1275?
Thinking about mathematics from someone else’s perspective than your own (which is the heart of being a teacher)
by Deborah Ball
49 x 25 = 1225
Below are three solutions to the same problem, each of which does not yield 1225 as the answer.
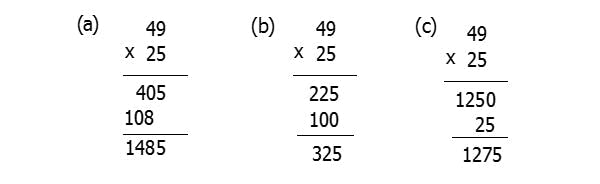
What mathematical steps could produce each of these three answers?
(a) 1485
What mathematical steps are involved? Multiply 9 x 5, which produces 45. Write down the 5 and carry the 4. Add the 4 to the other 4 in the tens column, which yields 8, and multiply 8 x 5, which is 40. Write down 40. Next, multiply 9 x 2, which equals 18. Write down 8 and carry the 1; as before, add the 1 to the 4 before multiplying, i.e., 5 x 2, which equals 10.
What is the main issue to understand? This process adds the carried ten in before multiplying, instead of afterwards.
In addition to being able to understand what happened, what other sort of mathematical understanding would a teacher need to have? A teacher would also have to be able to explain why it is not correct to add the carried number before multiplying; with addition, after all, it does not matter whether one adds the carried ten before or after adding the other numbers in the column.
(b) 325
What mathematical steps are involved? Multiply 25 x 9 first (bottom up). This yields 225. Then multiply 25 x 4, which equals 100.
What is the main issue to understand? This process starts with the bottom number instead of with the top as is conventional. This is mathematically valid because multiplicaiton is commutative and so the order in which one multiplies does not matter. However, 25 x 4 is really 25 x 40, which would produce 1000.
In addition to being able to understand what happened, what other sort of mathematical understanding would a teacher need to have? A teacher would need to understand and be able to explain this and not just say that the 100 needs to be “moved over,” which is not an explanation of what is wrong.
(c) 1275
What mathematical steps are involved? Round 49 up to 50, then multiply 50 x 25, which is 1250. Then add 25 to 1250 because 49 is less than 50.
What is the main issue to understand? This process compensates in the wrong direction –– i.e., adds 25 to the 1250 instead of subtracting. Someone might do this because with the conventional procedure one adds together the two separate answers.
In addition to being able to understand what happened, what other sort of mathematical understanding would a teacher need to have? A teacher would have to be explain how the rounding works and how to compensate correctly, and why one should subtract 25 from 1250 instead of adding.

